算法入门：复杂度、排序与二分查找

1. 时间与空间复杂度

在算法竞赛中，时间复杂度和空间复杂度是评估算法性能的关键指标，通常更侧重于时间复杂度。

1.1. 概述

时间复杂度： 描述算法的执行效率（运行时间）。越低越好。
空间复杂度： 描述算法占用的内存量。在算法竞赛中，时间复杂度通常是主要挑战，空间限制一般较宽松，但仍需注意。

1.2. 时间复杂度

1.2.1. 定义与表示法

时间复杂度描述了算法执行时间随输入数据规模 N 变化的趋势。我们使用大 O 表示法 O(f(N)) 来表示。

常见的时间复杂度函数（高中数学函数）：

$O (1)$ (常数时间)
$O (lo g N)$ (对数时间；底数通常不重要，所以 $O (lo g_{2} N)$ 或 $O (ln N)$ 都简化为 $O (lo g N)$ )
$O (N)$ (平方根时间)
$O (N)$ (线性时间)
$O (N lo g N)$ (线性对数时间)
$O (N^{2})$ (平方时间)
$O (N^{3})$ (立方时间)
$O (2^{N})$ (指数时间)
$O (N!)$ (阶乘时间)

函数性质：

在算法竞赛中，数据规模 N 通常是非负的（ $N \geq 1$ ），所以我们只考虑函数在第一象限的行为。
在第一象限，上面列出的函数都是递增的，意味着执行时间随 N 的增长而增长。
核心原则：忽略常数因子。 例如，O(2N) 和 O(5N) 都被视为 O(N)。这是因为大 O 表示法代表增长趋势，常数因子不影响渐近行为。
O(1) 的特殊性： 当操作次数是常数时（例如 A+B），我们用 O(1) 来表示。

1.2.2. 时间复杂度分析示例

寻找数组中的最小值

问题： 给定一个长度为 N 的数组 A，找到最小值。
逻辑： 遍历数组一次，维护当前的最小值。
数据范围： $N \leq 200, 000$ 。

伪代码结构：

C++

const int MAXN = 200000 + 5; // 常见做法，分配稍大的数组以防越界
int a[MAXN]; // 或使用 vector<int> a;
int n;
// cin >> n; // 读入 N
// 循环读入 a[1]...a[N] (算法竞赛推荐1-based索引)

int min_val = 2e9; // 初始化为正无穷 (2 * 10^9)
for (int i = 1; i <= n; ++i) { // 循环 N 次
    // min_val = min(min_val, a[i]); // 每次操作是常数时间
    if (a[i] < min_val) {
        min_val = a[i];
    }
}
// cout << min_val;

复杂度分析： 循环执行 N 次。循环内部的操作（比较、赋值、增量）都是常数时间。总操作数约为 $C \times N$ 。根据忽略常数的原则，时间复杂度为 $O (N)$ 。

最大公约数 (GCD) - 欧几里得算法

问题： 找到两个正整数 X 和 Y 的最大公约数。
算法原理： 基于 $GC D (X, Y) = GC D (Y, X (mod Y))$ ，以及 $GC D (X, 0) = X$ 。

示例代码 (递归)：

C++

int gcd(int x, int y) {
    if (y == 0) {
        return x;
    }
    return gcd(y, x % y); // 递归调用
}

复杂度分析： 在每一步递归中，Y 都在减小，并且保证至少会减半（与斐波那契数列的逆向相关）。因此，该算法的时间复杂度为 $O (lo g N)$ ，其中 N 是 X 和 Y 中较大的那个数。这里的对数底数不重要，因为 $lo g_{a} N = \frac{l o g _{b} N}{l o g _{b} a}$ ，意味着不同底数仅相差一个常数因子。

一个特殊的嵌套 For 循环

问题： 计算以下嵌套循环的执行次数。

代码示例：

C++

int n; // 假设 n 已经输入
long long c = 0; // 计数器
for (int i = 1; i <= n; ++i) {
    for (int j = i; j <= n; j += i) {
        c++; // 每次执行时增加计数器
    }
}
// cout << c; // 输出最终计数

复杂度分析：
- 外层循环变量 i 从 1 到 N。
- 内层循环变量 j 从 i 开始，每次增加 i，直到超过 N。
- 当 i=1 时，j 取 1, 2, ..., N，执行 N/1 = N 次。
- 当 i=2 时，j 取 2, 4, ..., N' (不超过N)，执行 N/2 次。
- 当 i=3 时，j 取 3, 6, ..., N''，执行 N/3 次。
- ...
- 当 i=N 时，j 取 N，执行 N/N = 1 次。
- 总执行次数为 $N /1 + N /2 + N /3 + \dots + N / N = N \times (1 + 1/2 + 1/3 + \dots + 1/ N)$ 。
- 括号中的部分是调和级数，其和约等于 $ln N$ (自然对数)。
- 因此，总执行次数约为 $N ln N$ 。时间复杂度为 $O (N lo g N)$ 。

1.3. 空间复杂度

空间复杂度衡量算法在执行过程中占用的临时存储空间。

单个变量： $O (1)$ (常数空间)。例如 int x;。
长度为 N 的数组： $O (N)$ (线性空间)。例如 int arr[N];。
N 行 M 列的二维数组： $O (N \times M)$ 。

通常，算法竞赛中的空间限制是足够的，除非题目明确要求空间优化。

2. 冒泡排序 (Bubble Sort)

冒泡排序是最基础、最直观的排序算法之一。虽然它的效率不高，但理解冒泡排序有助于掌握排序算法的基本思想。

核心思想

冒泡排序的工作原理是：

重复遍历要排序的数组
比较相邻元素，如果它们的顺序错误就交换它们
重复这个过程，直到没有需要交换的元素，说明数组已经有序

较大的元素会像"气泡"一样逐渐"浮"到数组的末尾，这也是"冒泡排序"名称的由来。

代码实现

基础版本：

C++

// 对数组 a[1...n] 进行冒泡排序
void bubble_sort(int a[], int n) {
    // 外层循环：需要 n-1 轮
    for (int i = 1; i < n; i++) {
        // 内层循环：每轮比较相邻元素
        for (int j = 1; j <= n - i; j++) {
            // 如果前面的元素大于后面的，交换它们
            if (a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
            }
        }
    }
}

优化版本（提前终止）：

C++

// 优化版冒泡排序
void bubble_sort_optimized(int a[], int n) {
    for (int i = 1; i < n; i++) {
        bool swapped = false; // 标记本轮是否发生交换
        
        for (int j = 1; j <= n - i; j++) {
            if (a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
                swapped = true;
            }
        }
        
        // 如果本轮没有发生交换，说明已经有序，提前退出
        if (!swapped) break;
    }
}

算法步骤详解

以数组 [5, 3, 8, 4, 2] 为例，展示冒泡排序的执行过程：

第 1 轮：（从左到右比较相邻元素）

比较 5 和 3：5 > 3，交换 → [3, 5, 8, 4, 2]
比较 5 和 8：5 < 8，不交换 → [3, 5, 8, 4, 2]
比较 8 和 4：8 > 4，交换 → [3, 5, 4, 8, 2]
比较 8 和 2：8 > 2，交换 → [3, 5, 4, 2, 8] ✓（最大值 8 就位）

第 2 轮：

比较 3 和 5：3 < 5，不交换 → [3, 5, 4, 2, 8]
比较 5 和 4：5 > 4，交换 → [3, 4, 5, 2, 8]
比较 5 和 2：5 > 2，交换 → [3, 4, 2, 5, 8] ✓（次大值 5 就位）

第 3 轮：

比较 3 和 4：3 < 4，不交换 → [3, 4, 2, 5, 8]
比较 4 和 2：4 > 2，交换 → [3, 2, 4, 5, 8] ✓

第 4 轮：

比较 3 和 2：3 > 2，交换 → [2, 3, 4, 5, 8] ✓（排序完成）

复杂度分析

时间复杂度：
- 平均： $O (n^{2})$ - 需要约 $n^{2} /2$ 次比较
- 最坏： $O (n^{2})$ - 数组完全逆序时
- 最好： $O (n)$ - 数组已有序（优化版本）
空间复杂度： $O (1)$ - 只需要常数级的额外空间
稳定性： 稳定 - 相等元素的相对位置不会改变

为什么不推荐冒泡排序？

虽然冒泡排序简单易懂，但在实际应用中几乎不使用，原因如下：

时间复杂度太高 - $O (n^{2})$ 的复杂度在大数据量时效率极低
实际性能差 - 即使是同为 $O (n^{2})$ 的算法，冒泡排序的常数因子也较大
有更好的选择 - 快速排序、归并排序等 $O (n lo g n)$ 算法效率更高

但是： 理解冒泡排序有助于理解排序的基本思想和算法分析方法，在学习阶段仍有重要价值。

3. 快速排序 (Quick Sort)

快速排序是一种基于"分治"（Divide and Conquer）思想的高效排序算法。

核心思想

分（Partition）：
- 从数组中选取一个元素作为“基准值”（Pivot）。
- 重新排列数组，将所有小于基准值的元素移动到基准值的左侧，所有大于基准值的元素移动到基准值的右侧。
治（Conquer）：
- 递归地对基准值左侧的子数组和右侧的子数组进行快速排序。
合（Combine）：
- 由于是原地排序，当子数组排序完成后，整个数组即完成排序，无需合并。

代码模板

C++

// a[] 是全局数组
void quick_sort(int l, int r) {
    if (l >= r) return; // 递归出口：区间内没有元素或只有一个元素

    // 1. 选取基准值 和 初始化指针
    int x = a[l + r >> 1], i = l - 1, j = r + 1;// a[l + r >> 1]是位运算，二进制值删去最后一位，相当于处以2，位运算符优先级比加减小，所以 l+r 不需要加括号

    // 2. 核心分区循环
    while (i < j) {
        // 3. 移动左指针
        while (a[++i] < x);
        // 4. 移动右指针
        while (a[--j] > x);
        
        // 5. 交换
        if (i < j) swap(a[i], a[j]);
    }

    // 6. 递归处理子区间
    quick_sort(l, j);
    quick_sort(j + 1, r);
}

步骤详解

基准值与指针 (第 5 行)
- if (l >= r) return;：这是递归的终止条件。如果左边界 l 已经等于或超过了右边界 r，说明这个区间最多只有一个元素，自然是有序的，直接返回。
- int x = a[l + r >> 1]：选取区间的中间位置的元素作为基准值 x。l + r >> 1 是 (l + r) / 2 的位运算写法，效率更高。
- i = l - 1, j = r + 1：这是此模板的精髓所在。i 和 j 指针分别从待排序区间的外侧开始。i 从左边界-1 开始，j 从右边界+1 开始。
分区循环 (第 8 行)
- while (i < j)：当左指针 i 仍然在右指针 j 的左侧时，继续分区。当 i >= j 时，分区结束。
移动左指针 (第 10 行)
- while (a[++i] < x);：先将 i 右移一位（++i），然后比较 a[i] 和 x。只要 a[i] 小于基准值 x，就继续右移。
- 循环结束时，i 会停在第一个大于等于 x 的元素的位置上。
移动右指针 (第 12 行)
- while (a[--j] > x);：先将 j 左移一位（--j），然后比较 a[j] 和 x。只要 a[j] 大于基准值 x，就继续左移。
- 循环结束时，j 会停在第一个小于等于 x 的元素的位置上。
交换 (第 15 行)
- if (i < j) swap(a[i], a[j]);：
- 此时，a[i] 是左侧找到的 "不该在左侧" 的元素（ $\geq x$ ），a[j] 是右侧找到的 "不该在右侧" 的元素（ $\leq x$ ）。
- 如果 i < j，说明 i 还在 j 的左边，两者尚未相遇，所以我们交换它们，将它们放到正确的分区。
- 如果 i >= j，说明两个指针已经相遇或交错，分区过程结束，跳出 while (i < j) 循环。
递归 (第 19-20 行)
- quick_sort(l, j);
- quick_sort(j + 1, r);
- 为什么是 j 和 j+1？ 这是此模板的第二个精髓。
- 当 while (i < j) 循环结束时，j 左侧（包括 j）的所有元素都小于等于基准值 x，j 右侧的所有元素都大于等于基准值 x。
- 因此，我们将数组分为 [l, j] 和 [j + 1, r] 两个子区间，分别进行递归排序。
- 思考： 为什么不用 i 来划分？因为当循环结束时，i 和 j 可能重合（i == j），也可能交错（i == j + 1）。但无论哪种情况，j 始终是左侧分区的“分界点”。使用 [l, j] 和 [j+1, r] 来划分区间，可以完美覆盖所有情况，不多也不少。

复杂度

时间复杂度：
- 平均： $O (n lo g n)$
- 最坏： $O (n^{2})$ （当数组已经有序或接近有序，且基准值总选到最大/最小值时）
空间复杂度： $O (lo g n)$ （递归栈的深度）
稳定性： 不稳定

4. 归并排序 (Merge Sort)

归并排序是另一种基于"分治"思想的排序算法，它以稳定、高效著称。

核心思想

分（Divide）： 不断将当前数组对半切分，直到每个子数组只剩一个元素（天然有序）。
治（Conquer）： 这一步在归并排序中体現在“合”的阶段。
合（Merge）： 将两个已经有序的子数组，合并成一个新的、更大的有序数组。

代码模板解析

Plain Text

// a[] 和 N 是全局的
void merge_sort(int l, int r) {
    if (l >= r) return; // 递归出口

    // 1. 临时数组，用于合并
    int temp[N]; 
    
    // 2. 分：计算中点并递归
    int mid = l + r >> 1;
    merge_sort(l, mid);
    merge_sort(mid + 1, r);

    // 3. 合：合并两个有序子数组 [l, mid] 和 [mid+1, r]
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r) {
        if (a[i] < a[j]) temp[k++] = a[i++];
        else temp[k++] = a[j++];
    }

    // 4. 处理剩余元素
    while (i <= mid) temp[k++] = a[i++];
    while (j <= r) temp[k++] = a[j++];

    // 5. 将排好序的 temp 数组复制回原数组 a
    for (int i = l, j = 0; i <= r; i++, j++) a[i] = temp[j];
}

步骤详解

临时数组 (第 5 行)
- int temp[N];：归并排序的核心代价在于需要一个额外的 $O (n)$ 空间。temp 数组用于在“合并”阶段临时存放排好序的元素。
- 注意： 你给的模板在递归函数内部声明了 temp。这意味着每次递归调用都会声明一个 temp 数组，这在空间上是低效的（虽然功能上没错）。更优化的写法是将 temp 作为全局变量或在 merge_sort 之外声明，通过参数传入。但我们这里只解析你给的模板。
分 (第 8-10 行)
- int mid = l + r >> 1;：计算中点。
- merge_sort(l, mid), merge_sort(mid + 1, r);：递归地对左右两个子区间进行排序。当这两行代码执行完毕后，我们可以保证 a[l...mid] 和 a[mid+1...r] 两个子数组各自内部已经是有序的了。
合 (第 13-17 行)
- k = 0, i = l, j = mid + 1;：i 是左半边有序数组的指针，j 是右半边有序数组的指针，k 是 temp 数组的指针。
- while (i <= mid && j <= r)：当两个子数组都还有元素时，进行比较。
- if (a[i] < a[j])...：将 a[i] 和 a[j] 中较小的那个元素放入 temp 数组，并移动相应的指针。
处理剩余 (第 20-21 行)
- 上面的 while 循环结束后，i 和 j 中必定有一个指针已经越界（即它所指向的子数组已经全部存入 temp）。
- 这两个 while 循环的作用是，将另一个未越界的子数组中剩余的元素（它们本身已经有序且都大于已存入 temp 的元素）全部复制到 temp 数组的末尾。
复制回原数组 (第 24 行)
- for (int i = l, j = 0; i <= r; i++, j++) a[i] = temp[j];
- 这是至关重要的一步。此时 temp 数组的 [0...k-1]（即 temp[0...r-l]）中存放的是 a[l...r] 区间合并排序后的结果。
- 这个循环将 temp 中的元素按顺序复制回原数组 a 的 [l...r] 位置。注意 i 从 l 开始，j 从 0 开始。

复杂度

时间复杂度： $O (n lo g n)$ （无论最好最坏，都非常稳定）
空间复杂度： $O (n)$ （需要 temp 数组）
稳定性： 稳定（在 a[i] < a[j] 的判断中，如果不加等号，可以保证相等元素的相对顺序不变）

(〃∀〃)
恭喜！你刚刚学完了两种最核心的 $O (n lo g n)$ 排序算法。
然而，在 99% 的实际开发和算法竞赛中...
忘掉它们（bushi），然后无脑用 C++ 的 std::sort 就完事了！
它更快（经过高度优化）、更安全（规避了最坏情况）、更省心（sort(a, a+n); 一行搞定）。
（严肃脸：当然，归并排序的"稳定"特性和"分治"思想本身还是需要牢记的！面试要考！）

5. 二分查找 (Binary Search)

二分查找（或称折半查找）是一种在有序数组中查找某一特定元素的搜索算法。它的核心思想是不断地将搜索区间减半。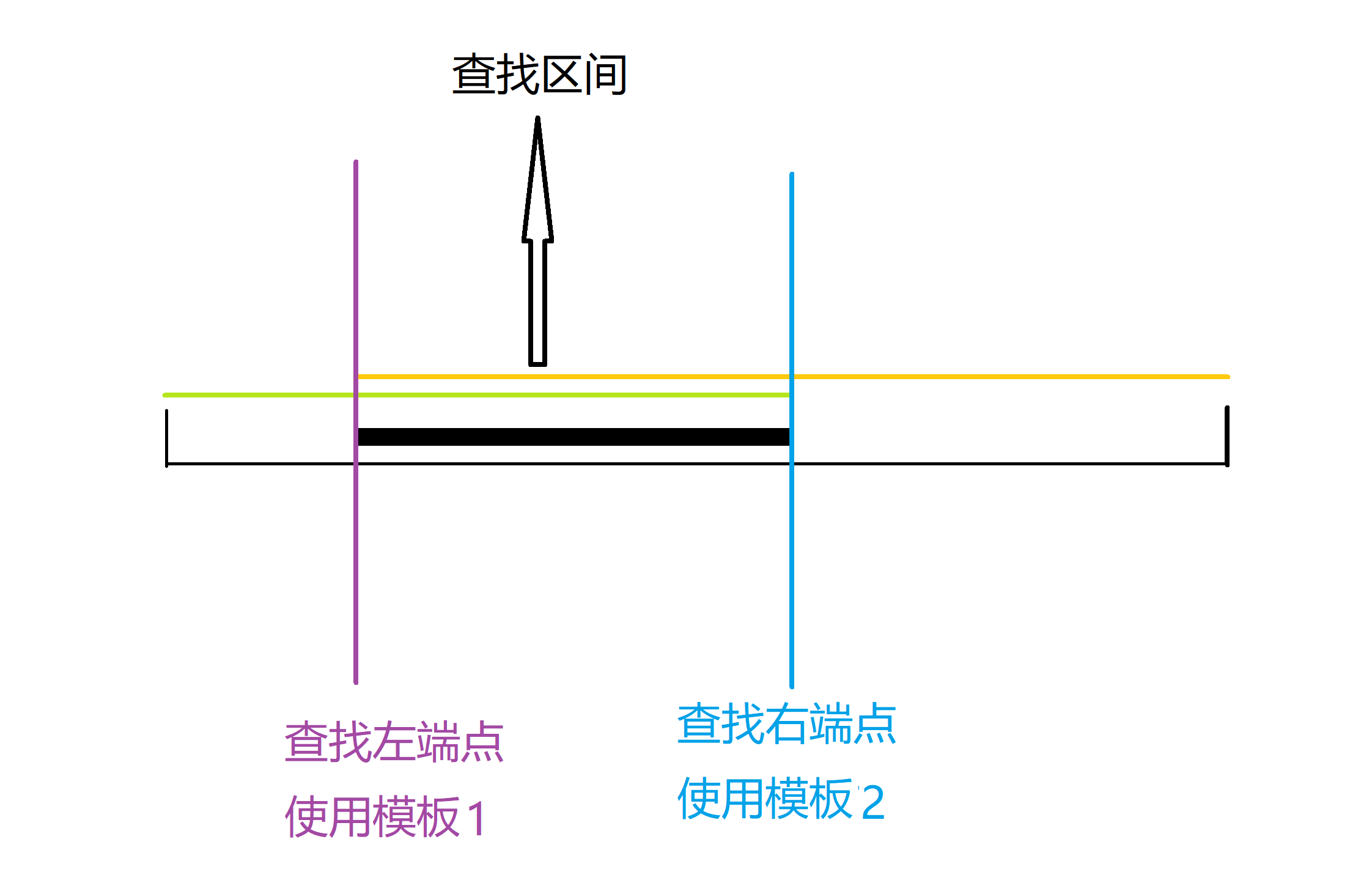

下面有两个模板，它们分别用于解决两种最常见的二分问题：

模板1： 在一个区间内找到满足某个条件的最小（最左侧）的值。
模板2： 在一个区间内找到满足某个条件的最大（最右侧）的值。

模板 1：查找左边界

Plain Text

// 检查 q[mid] 是否 "大于等于 x"
// 区间 [l, r] 被划分为 [l, mid] 和 [mid+1, r]
// check 函数是判断要找的值是否符合条件
while (l < r) {
    int mid = l + r >> 1; // (l+r)/2，向下取整
    if (check(q[mid])) r = mid; // check为true，答案可能在[l, mid]
    else l = mid + 1; // check为false，答案一定在[mid+1, r]
}
// 循环结束时 l == r，即为答案

用途： 查找第一个满足 check() 为 true 的位置。

例如：在一个升序数组中，找到第一个 $\geq x$ 的数。

流程解析：

int mid = l + r >> 1;：mid 向下取整。
if (check(q[mid])) r = mid;
- 如果 q[mid] 满足条件（例如 q[mid] >= x），说明 mid 有可能是我们要找的那个 "最左侧" 的答案，或者答案在 mid 的左边。
- 我们不能排除 mid，所以我们将搜索区间的右边界缩小为 r = mid。新的搜索区间是 [l, mid]。
else l = mid + 1;
- 如果 q[mid] 不满足条件（例如 q[mid] < x），说明 mid 一定不是答案，并且 mid 左侧的所有元素也一定不是答案。
- 所以我们将搜索区间的左边界扩大为 l = mid + 1。新的搜索区间是 [mid + 1, r]。

为什么不会死循环？

当 l 和 r 只差 1 时，即 l = r - 1。
此时 mid = (l + l + 1) >> 1 = l。
if (check(q[l]))：r = l，循环结束。
else：l = l + 1，l 变成 r，循环结束。
两种情况都能正常退出。

模板 2：查找右边界

Plain Text

// 检查 q[mid] 是否 "小于等于 x"
// 区间 [l, r] 被划分为 [l, mid-1] 和 [mid, r]
// check 函数是判断要找的值是否符合条件
while (l < r) {
    int mid = l + r + 1 >> 1; // (l+r+1)/2，向上取整
    if (check(q[mid])) l = mid; // check为true，答案可能在[mid, r]
    else r = mid - 1; // check为false，答案一定在[l, mid-1]
}
// 循环结束时 l == r，即为答案

用途： 查找最后一个满足 check() 为 true 的位置。

例如：在一个升序数组中，找到最后一个 $\leq x$ 的数。

流程解析：

int mid = l + r + 1 >> 1;：这是此模板的精髓！ mid 向上取整。
if (check(q[mid])) l = mid;
- 如果 q[mid] 满足条件（例如 q[mid] <= x），说明 mid 有可能是我们要找的那个 "最右侧" 的答案，或者答案在 mid 的右边。
- 我们不能排除 mid，所以我们将搜索区间的左边界扩大为 l = mid。新的搜索区间是 [mid, r]。
else r = mid - 1;
- 如果 q[mid] 不满足条件（例如 q[mid] > x），说明 mid 一定不是答案，并且 mid 右侧的所有元素也一定不是答案。
- 所以我们将搜索区间的右边界缩小为 r = mid - 1。新的搜索区间是 [l, mid - 1]。

为什么必须 + 1？（防止死循环）

假设我们不加 + 1，即 mid = l + r >> 1（向下取整）。
考虑当 l 和 r 只差 1 时，即 l = r - 1。
此时 mid = (l + l + 1) >> 1 = l。
if (check(q[l]))：l = mid = l。l 和 r 的值都没有改变。
else：r = l - 1，循环会结束。
问题在于： 如果 check(q[l]) 总是为 true，l 将永远等于 mid，l 和 r 的值都不会变，while (l < r) 将无限循环！
解决方案：
我们使用 mid = l + r + 1 >> 1（向上取整）。
当 l = r - 1 时，mid = (l + l + 1 + 1) >> 1 = (2l + 2) >> 1 = l + 1 = r。
if (check(q[r]))：l = mid = r，l == r，循环结束。
else：r = mid - 1 = r - 1 = l，l == r，循环结束。
两种情况都能正常退出。

总结 (二分)：

当你的更新逻辑是 l = mid 时，mid 必须向上取整（+ 1）。
当你的更新逻辑是 r = mid 时，mid 必须向下取整（不 + 1）。

6. 总结对比 (所有算法)

算法	核心思想	平均时间	最坏时间	空间	稳定性	备注
冒泡排序	交换	$O (n^{2})$	$O (n^{2})$	$O (1)$	稳定	简单但低效，仅用于学习
快速排序	分治	$O (n lo g n)$	$O (n^{2})$	$O (lo g n)$	不稳定	原地排序，实现精妙
归并排序	分治	$O (n lo g n)$	$O (n lo g n)$	$O (n)$	稳定	时间稳定，但需额外空间
二分查找	减治	$O (lo g n)$	$O (lo g n)$	$O (1)$	N/A	前提：数组必须有序
`std::sort`	混合排序	$O (n lo g n)$ !	$O (n lo g n)$	$O (lo g n)$	不稳定	（推荐） C++标准库
`std::stable_sort`	归并排序	$O (n lo g n)$	$O (n lo g n)$	$O (n)$	稳定	C++标准库

7. 例题

1. 排序

P1923 【深基9.例4】求第 k 小的数

题目描述

输入 $n$ （ $1 \leq n < 5000000$ 且 $n$ 为奇数）个数字 $a_{i}$ （ $1 \leq a_{i} < 10^{9}$ ），输出这些数字的第 $k$ 小的数。最小的数是第 $0$ 小。

请尽量不要使用 nth_element 来写本题，因为本题的重点在于练习分治算法。

输入格式

第一行有两个整数，分别表示 $n$ 和 $k$ 。

第二行有 $n$ 个整数，第 $i$ 个数表示 $a_{i}$ 。

输出格式

一个整数，表示第 $k$ 小的数。

输入输出样例 #1

输入 #1

Plain Text

5 1
4 3 2 1 5

输出 #1

Plain Text

C++

#include<bits/stdc++.h>
using namespace std;
int miku[5000000];
void fufu(int a,int b){
    int mid=miku[(a+b)/2],i=a,j=b;
    while (i<=j){
        while(miku[i]<mid) i++;
        while(miku[j]>mid) j--;
        if (i<=j){
            swap(miku[i],miku[j]);
            i++;
            j--;
        }
    }
    if (i<b)fufu(i,b);
    if (j>a)fufu(a,j);
}
int main(){
    int n,k;
    scanf("%d %d",&n,&k);
    for (int i=0;i<n;i++){
        scanf("%d",&miku[i]);
    }
    fufu(0,n-1);
    printf("%d",miku[k]);
    return 0;
}

2. 二分

P1024 [NOIP 2001 提高组] 一元三次方程求解

题目描述

有形如： $a x^{3} + b x^{2} + c x + d = 0$ 这样的一个一元三次方程。给出该方程中各项的系数（ $a, b, c, d$ 均为实数），并约定该方程存在三个不同实根（根的范围在 $- 100$ 至 $100$ 之间），且根与根之差的绝对值 $\geq 1$ 。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格)，并精确到小数点后 $2$ 位。

提示：记方程 $f (x) = 0$ ，若存在 $2$ 个数 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ， $f (x_{1}) \times f (x_{2}) < 0$ ，则在 $(x_{1}, x_{2})$ 之间一定有一个根。

输入格式

一行， $4$ 个实数 $a, b, c, d$ 。

输出格式

一行， $3$ 个实根，从小到大输出，并精确到小数点后 $2$ 位。

输入输出样例 #1

输入 #1

Plain Text

1 -5 -4 20

输出 #1

Plain Text

-2.00 2.00 5.00

说明/提示

【题目来源】

NOIP 2001 提高组第一题

C++

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
double a,b,c,d;
int sum=0;
double check(double x){
    double s=a*x*x*x+b*x*x+c*x+d;
    return s;
}
int main(){
    cin>>a>>b>>c>>d;
    for(double i=-100.0;i<100.0;i+=0.001){
        if(check(i)-0<1e-4&&0-check(i)<1e-4){
            printf("%.2lf ",i);
            sum++;
            if(sum==3)break;
        }
    }
    return 0;
}

P2440 木材加工

题目背景

要保护环境。

题目描述

木材厂有 $n$ 根原木，现在想把这些木头切割成 $k$ 段长度均为 $l$ 的小段木头（木头有可能有剩余）。

当然，我们希望得到的小段木头越长越好，请求出 $l$ 的最大值。

木头长度的单位是 $cm$ ，原木的长度都是正整数，我们要求切割得到的小段木头的长度也是正整数。

例如有两根原木长度分别为 $11$ 和 $21$ ，要求切割成等长的 $6$ 段，很明显能切割出来的小段木头长度最长为 $5$ 。

输入格式

第一行是两个正整数 $n, k$ ，分别表示原木的数量，需要得到的小段的数量。

接下来 $n$ 行，每行一个正整数 $L_{i}$ ，表示一根原木的长度。

输出格式

仅一行，即 $l$ 的最大值。

如果连 $1cm$ 长的小段都切不出来，输出 0。

输入输出样例 #1

输入 #1

Plain Text

输出 #1

Plain Text

说明/提示

数据规模与约定

对于 $100%$ 的数据，有 $1 \leq n \leq 1 0^{5}$ ， $1 \leq k \leq 1 0^{8}$ ， $1 \leq L_{i} \leq 1 0^{8} (i \in [1, n])$ 。

C++

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e8+10;
int miku[N];
int n,k;
bool check(int x){
    int s=0;
    for(int i=0;i<n;i++){
        s+=miku[i]/x;
    }
    if(s>=k)return true;
    return false;
}
int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>miku[i];
    }
    sort(miku,miku+n);
    int l=0,r=miku[n-1];
    while(l<r){
        int mid=l+r+1>>1;
        if(!check(mid))r=mid-1;
        else l=mid;
    }
    cout<<l;
    return 0;
}

算法入门：复杂度、排序与二分查找 ​

1. 时间与空间复杂度 ​

1.1. 概述 ​

1.2. 时间复杂度 ​

1.2.1. 定义与表示法 ​

1.2.2. 时间复杂度分析示例 ​

1.3. 空间复杂度 ​

2. 冒泡排序 (Bubble Sort) ​

核心思想 ​

代码实现 ​

算法步骤详解 ​

复杂度分析 ​

为什么不推荐冒泡排序？ ​

3. 快速排序 (Quick Sort) ​

核心思想 ​

代码模板 ​

步骤详解 ​

复杂度 ​

4. 归并排序 (Merge Sort) ​

核心思想 ​

代码模板解析 ​

步骤详解 ​

复杂度 ​

(〃∀〃) ​

5. 二分查找 (Binary Search) ​

模板 1：查找左边界 ​

模板 2：查找右边界 ​

6. 总结对比 (所有算法) ​

7. 例题 ​

1. 排序 ​

P1923 【深基9.例4】求第 k 小的数 ​

题目描述 ​

输入格式 ​

输出格式 ​

输入输出样例 #1 ​

2. 二分 ​

P1024 [NOIP 2001 提高组] 一元三次方程求解 ​

题目描述 ​

输入格式 ​

输出格式 ​

输入输出样例 #1 ​

说明/提示 ​

P2440 木材加工 ​

题目背景 ​

题目描述 ​

输入格式 ​

输出格式 ​

输入输出样例 #1 ​

说明/提示 ​

数据规模与约定 ​

算法入门：复杂度、排序与二分查找

1. 时间与空间复杂度

1.1. 概述

1.2. 时间复杂度

1.2.1. 定义与表示法

1.2.2. 时间复杂度分析示例

1.3. 空间复杂度

2. 冒泡排序 (Bubble Sort)

核心思想

代码实现

算法步骤详解

复杂度分析

为什么不推荐冒泡排序？

3. 快速排序 (Quick Sort)

核心思想

代码模板

步骤详解

复杂度

4. 归并排序 (Merge Sort)

核心思想

代码模板解析

步骤详解

复杂度

(〃∀〃)

5. 二分查找 (Binary Search)

模板 1：查找左边界

模板 2：查找右边界

6. 总结对比 (所有算法)

7. 例题

1. 排序

P1923 【深基9.例4】求第 k 小的数

题目描述

输入格式

输出格式

输入输出样例 #1

2. 二分

P1024 [NOIP 2001 提高组] 一元三次方程求解

题目描述

输入格式

输出格式

输入输出样例 #1

说明/提示

P2440 木材加工

题目背景

题目描述

输入格式

输出格式

输入输出样例 #1

说明/提示

数据规模与约定